On the Internet, including Habré, you can find a lot of information about the Kalman filter. But it is hard to find an easily digestible derivation of the formulas themselves. Without a conclusion, all this science is perceived as a kind of shamanism, the formulas look like a faceless set of symbols, and most importantly, many simple statements that lie on the surface of the theory are beyond understanding. The purpose of this article will be to talk about this filter in the most accessible language.
The Kalman filter is a powerful data filtering tool. Its main principle is that when filtering, information about the physics of the phenomenon itself is used. Let's say if you're filtering data from a car's speedometer, then the inertia of the car gives you the right to perceive too fast speed jumps as a measurement error. The Kalman filter is interesting because, in a sense, it is the best filter. We will discuss in more detail below what exactly the words “the best” mean. At the end of the article, I will show that in many cases the formulas can be simplified to such an extent that almost nothing remains of them.

Likbez

Before getting acquainted with the Kalman filter, I propose to recall some simple definitions and facts from probability theory.

Random value

When they say that a random variable is given, they mean that this variable can take on random values. It takes on different values ​​with different probabilities. When you throw, say, a die, a discrete set of values ​​will fall out: . When it comes to, for example, the speed of a wandering particle, then, obviously, one has to deal with a continuous set of values. “Dropped out” values ​​of a random variable will be denoted by , but sometimes we will use the same letter that denotes a random variable: .
In the case of a continuous set of values, the random variable is characterized by the probability density , which dictates to us that the probability that the random variable "falls out" in a small neighborhood of a point of length is equal to . As we can see from the picture, this probability is equal to the area of ​​the shaded rectangle under the graph:

Quite often in life, random variables are distributed according to Gauss, when the probability density is .

We see that the function has the shape of a bell centered at a point and with a characteristic width of the order of .
Since we are talking about the Gaussian distribution, it would be a sin not to mention where it came from. Just as numbers are firmly established in mathematics and appear in the most unexpected places, so the Gaussian distribution has taken deep roots in probability theory. One remarkable statement that partially explains Gaussian omnipresence is the following:
Let there be a random variable having an arbitrary distribution (in fact, there are some restrictions on this arbitrariness, but they are not at all rigid). Let's carry out experiments and calculate the sum of the "dropped out" values ​​of a random variable. Let's do a lot of these experiments. It is clear that each time we will receive a different value of the sum. In other words, this sum is in itself a random variable with its own certain distribution law. It turns out that for sufficiently large, the distribution law of this sum tends to the Gaussian distribution (by the way, the characteristic width of the “bell” grows as ). Read more on wikipedia: central limit theorem. In life, very often there are quantities that are made up of a large number of equally distributed independent random variables, and therefore are distributed according to Gauss.

Mean

The average value of a random variable is what we get in the limit if we conduct a lot of experiments and calculate the arithmetic mean of the dropped values. The average value is denoted in different ways: mathematicians like to denote by (expectation), and foreign mathematicians by (expectation). Physics same through or. We will designate in a foreign way:.
For example, for a Gaussian distribution , the mean is .

Dispersion

In the case of the Gaussian distribution, we can clearly see that the random variable prefers to fall out in some neighborhood of its mean value . As can be seen from the graph, the characteristic scatter of order values ​​is . How can we estimate this spread of values ​​for an arbitrary random variable if we know its distribution. You can draw a graph of its probability density and estimate the characteristic width by eye. But we prefer to go the algebraic way. You can find the average length of the deviation (modulus) from the average value: . This value will be a good estimate of the characteristic spread of values ​​. But you and I know very well that using modules in formulas is a headache, so this formula is rarely used to estimate the characteristic spread.
An easier way (simple in terms of calculations) is to find . This quantity is called the variance and is often referred to as . The root of the variance is called the standard deviation. The standard deviation is a good estimate of the spread of a random variable.
For example, for a Gaussian distribution, we can assume that the variance defined above is exactly equal to , which means that the standard deviation is equal to , which agrees very well with our geometric intuition.
In fact, there is a small scam hidden here. The fact is that in the definition of the Gaussian distribution, under the exponent is the expression . This two in the denominator is precisely so that the standard deviation would be equal to the coefficient. That is, the Gaussian distribution formula itself is written in a form specially sharpened for the fact that we will consider its standard deviation.

Independent random variables

Random variables may or may not be dependent. Imagine that you throw a needle on a plane and write down the coordinates of both ends of it. These two coordinates are dependent, they are connected by the condition that the distance between them is always equal to the length of the needle, although they are random variables.
Random variables are independent if the outcome of the first one is completely independent of the outcome of the second one. If the random variables and are independent, then the average value of their product is equal to the product of their average values:

Proof

For example, having blue eyes and finishing school with a gold medal are independent random variables. If blue-eyed, say a gold medalists , then blue-eyed medalists This example tells us that if random variables and are given by their probability densities and , then the independence of these quantities is expressed in the fact that the probability density (the first value dropped out , and the second ) is found by the formula:

It immediately follows from this that:

As you can see, the proof is carried out for random variables that have a continuous spectrum of values ​​and are given by their probability density. In other cases, the idea of ​​the proof is similar.

Kalman filter

Formulation of the problem

Denote by the value that we will measure and then filter. It can be coordinate, speed, acceleration, humidity, stink degree, temperature, pressure, etc.
Let's start with a simple example, which will lead us to the formulation of a general problem. Imagine that we have a radio-controlled car that can only go forward and backward. We, knowing the weight of the car, shape, road surface, etc., calculated how the controlling joystick affects the speed of movement.

Then the coordinate of the machine will change according to the law:

In real life, we cannot take into account in our calculations small perturbations acting on the car (wind, bumps, pebbles on the road), so the real speed of the car will differ from the calculated one. A random variable is added to the right side of the written equation:

We have a GPS sensor installed on the car, which tries to measure the true coordinate of the car, and, of course, cannot measure it exactly, but measures it with an error, which is also a random variable. As a result, we get erroneous data from the sensor:

The problem is that, knowing the incorrect sensor readings, find a good approximation for the true coordinate of the machine.
In the formulation of the general problem, anything can be responsible for the coordinate (temperature, humidity ...), and we will denote the term responsible for controlling the system from the outside as (in the example with the machine). The equations for the coordinate and sensor readings will look like this:

Let's discuss in detail what we know:

It is useful to note that the filtering task is not a smoothing task. We do not aim to smooth the data from the sensor, we aim to get the closest value to the real coordinate .

Kalman algorithm

We will reason by induction. Imagine that at the -th step we have already found the filtered value from the sensor , which approximates well the true coordinate of the system . Do not forget that we know the equation that controls the change in an unknown coordinate:

therefore, without getting the value from the sensor yet, we can assume that at the step the system evolves according to this law and the sensor will show something close to . Unfortunately, we can't say anything more precise yet. On the other hand, at the step we will have an inaccurate sensor reading on our hands.
Kalman's idea is as follows. To get the best approximation to the true coordinate , we must choose a happy medium between the inaccurate sensor reading and our prediction of what we expected it to see. We will give the sensor reading a weight and the predicted value will have a weight:

The coefficient is called the Kalman coefficient. It depends on the iteration step, so it would be more correct to write , but for now, in order not to clutter up the calculation formulas, we will omit its index.
We must choose the Kalman coefficient in such a way that the resulting optimal value of the coordinate would be closest to the true value. For example, if we know that our sensor is very accurate, then we will trust its reading more and give the value more weight (close to one). If the sensor, on the contrary, is not at all accurate, then we will focus more on the theoretically predicted value of .
In general, to find the exact value of the Kalman coefficient, one simply needs to minimize the error:

We use equations (1) (the ones in the blue box) to rewrite the expression for the error:

Proof

Now is the time to discuss what does the expression minimize error mean? After all, the error, as we see, is itself a random variable and each time takes on different values. There really isn't a one-size-fits-all approach to defining what it means for the error to be minimal. Just as in the case of the variance of a random variable, when we tried to estimate the characteristic width of its scatter, here we will choose the simplest criterion for calculations. We will minimize the mean from the squared error:

Let's write the last expression:

Proof

From the fact that all random variables included in the expression for are independent, it follows that all "cross" terms are equal to zero:

We used the fact that , then the formula for the variance looks much simpler: .

This expression takes on a minimum value when (equate the derivative to zero):

Here we are already writing an expression for the Kalman coefficient with step index , thus we emphasize that it depends on the iteration step.
We substitute the obtained optimal value into the expression for which we have minimized. We receive;

Our task is solved. We have obtained an iterative formula for calculating the Kalman coefficient.
Let's summarize our acquired knowledge in one frame:

Example

Matlab code

clear all; N=100% number of samples a=0.1% acceleration sigmaPsi=1 sigmaEta=50; k=1:N x=k x(1)=0 z(1)=x(1)+normrnd(0,sigmaEta); for t=1:(N-1) x(t+1)=x(t)+a*t+normrnd(0,sigmaPsi); z(t+1)=x(t+1)+normrnd(0,sigmaEta); end; %kalman filter xOpt(1)=z(1); eOpt(1)=sigmaEta; for t=1:(N-1) eOpt(t+1)=sqrt((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+ sigmaPsi^2)) K(t+1)=(eOpt(t+1))^2/sigmaEta^2 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t +1))+K(t+1)*z(t+1) end; plot(k,xopt,k,z,k,x)

Analysis

If we trace how the Kalman coefficient changes with the iteration step, then we can show that it always stabilizes to a certain value. For example, when the RMS errors of the sensor and the model relate to each other as ten to one, then the plot of the Kalman coefficient depending on the iteration step looks like this:

In the following example, we will discuss how this can make our lives much easier.

Second example

In practice, it often happens that we do not know anything at all about the physical model of what we are filtering. For example, you want to filter readings from your favorite accelerometer. You do not know in advance by what law you intend to turn the accelerometer. The most information you can glean is the sensor error variance. In such a difficult situation, all ignorance of the motion model can be driven into a random variable:

But, frankly, such a system no longer satisfies the conditions that we imposed on the random variable , because now all the physics of motion unknown to us is hidden there, and therefore we cannot say that at different points in time, the errors of the model are independent of each other and that their mean values ​​are zero. In this case, by and large, the theory of the Kalman filter is not applicable. But, we will not pay attention to this fact, but, stupidly apply all the colossus of formulas, choosing the coefficients and by eye, so that the filtered data looks pretty.
But there is another, much easier way to go. As we saw above, the Kalman coefficient always stabilizes to the value . Therefore, instead of selecting the coefficients and and finding the Kalman coefficient using complex formulas, we can consider this coefficient to be always a constant, and select only this constant. This assumption will spoil almost nothing. Firstly, we are already illegally using the Kalman theory, and secondly, the Kalman coefficient quickly stabilizes to a constant. In the end, everything will be very simple. We don’t need any formulas from Kalman’s theory at all, we just need to choose an acceptable value and insert it into the iterative formula:

The following graph shows data from a fictitious sensor filtered in two different ways. Provided that we know nothing about the physics of the phenomenon. The first way is honest, with all the formulas from Kalman's theory. And the second one is simplified, without formulas.

As we can see, the methods are almost the same. A small difference is observed only at the beginning, when the Kalman coefficient has not yet stabilized.

Discussion

As we have seen, the main idea of ​​the Kalman filter is to find a coefficient such that the filtered value

on average would differ least of all from the real value of the coordinate . We see that the filtered value is a linear function of the sensor reading and the previous filtered value . And the previous filtered value is, in turn, a linear function of the sensor reading and the previous filtered value . And so on, until the chain is completely unfolded. That is, the filtered value depends on all previous sensor readings linearly:

Therefore, the Kalman filter is called a linear filter.
It can be proved that the Kalman filter is the best of all linear filters. The best in the sense that the mean square of the filter error is minimal.

Multivariate case

The whole Kalman filter theory can be generalized to the multidimensional case. The formulas there look a little scarier, but the very idea of ​​their derivation is the same as in the one-dimensional case. You can see them in this excellent article: http://habrahabr.ru/post/140274/ .
And in this wonderful video an example of how to use them.

Kalman filter

The Kalman filter is widely used in engineering and econometric applications, from radar and vision systems to macroeconomic model parameter estimations. Kalman filtering is an important part of control theory and plays a large role in the creation of control systems. Together with a linear-quadratic controller, the Kalman filter allows solving the problem of linear-quadratic Gaussian control. Kalman filter and linear-quadratic controller - a possible solution to most fundamental problems in control theory.

In most applications, the number of parameters that define the state of an object is greater than the number of observable parameters available for measurement. With the help of the object model for a number of available measurements, the Kalman filter allows you to get an estimate of the internal state.

The Kalman filter is intended for recursive underestimation of the state vector of an a priori known dynamic system, that is, to calculate the current state of the system, it is necessary to know the current measurement, as well as the previous state of the filter itself. Thus, the Kalman filter, like many other recursive filters, is implemented in time rather than frequency representation.

A clear example of the filter's capabilities is obtaining accurate, continuously updated estimates of the position and speed of an object based on the results of a time series of inaccurate measurements of its location. For example, in radar the task is to track a target, determine its location, speed and acceleration, while the measurement results come gradually and are very noisy. The Kalman filter uses a probabilistic target dynamics model that specifies the type of object likely to move, which reduces the impact of noise and gives good estimates of the position of the object at the present, future or past moment in time.

Introduction

The Kalman filter operates with the concept of the system state vector (a set of parameters describing the state of the system at some point in time) and its statistical description. In the general case, the dynamics of some state vector is described by the probability densities of the distribution of its components at each moment of time. If there is a certain mathematical model of the observations of the system, as well as a model of a priori change in the parameters of the state vector (namely, as a Markov forming process), it is possible to write an equation for the a posteriori probability density of the state vector at any time. This differential equation is called the Stratonovich equation. The Stratonovich equation in general form is not solved. An analytical solution can be obtained only in the case of a number of restrictions (assumptions):

• Gaussian a priori and a posteriori probability densities of the state vector at any time (including the initial one)
• Gaussian shaping noise
• Gaussianity of observation noise
• observation noise whiteness
• observation model linearity
• linearity of the model of the forming process (which, we recall, must be a Markov process)

The classical Kalman filter is an equation for calculating the first and second moments of the posterior probability density (in the sense of the vector of mathematical expectations and the matrix of variances, including mutual ones) under given constraints. Since, for a normal probability density, the expectation and the variance matrix completely define the probability density, we can say that the Kalman filter calculates the posterior probability density of the state vector at each point in time. This means that it completely describes the state vector as a random vector quantity.

The calculated values ​​of mathematical expectations in this case are optimal estimates according to the criterion of root-mean-square error, which causes its wide application.

There are several varieties of the Kalman filter, which differ in approximations and tricks that have to be applied to reduce the filter to the described form and reduce its dimension:

• Extended Kalman filter (EKF, Extended Kalman filter). Reconciliation of Nonlinear Observation Models and the Formative Process by Linearization via Taylor Series Expansion.
• Unscented Kalman filter (UKF). It is used in problems in which simple linearization leads to the destruction of useful links between the components of the state vector. In this case, the "linearization" is based on an unscented -transform.
• Ensemble Kalman filter (EnKF). Used to reduce the dimension of the problem.
• Variants with a non-linear additional filter are possible, which make it possible to reduce non-Gaussian observations to normal ones.
• There are options with a "whitening" filter that allows you to work with "colored" noise
• etc.

Used dynamic system model

Kalman filters are based on time-sampled linear dynamical systems. Such systems are modeled by Markov chains using linear operators and terms with normal distribution. The state of the system is described by a vector of finite dimension - the state vector. At each time step, the linear operator acts on the state vector and transfers it to another state vector (deterministic state change), some normal noise vector (random factors) and, in the general case, a control vector that simulates the impact of the control system are added. The Kalman filter can be viewed as an analogue of hidden Markov models, with the difference that the variables describing the state of the system are elements of an infinite set of real numbers (in contrast to the finite set of the state space in hidden Markov models). In addition, hidden Markov models can use arbitrary distributions for subsequent state vector values, in contrast to the Kalman filter, which uses a normally distributed noise model. There is a strict relationship between the equations of the Kalman filter and the hidden Markov model. A review of these and other models is given by Roweis and Chahramani (1999) .

When using the Kalman filter to obtain estimates of the process state vector from a series of noisy measurements, it is necessary to represent the model of this process in accordance with the filter structure - in the form of a matrix equation of a certain type. For every beat k the filter operation, it is necessary to determine the matrices in accordance with the description below: process evolution F k; observation matrix H k; process covariance matrix Q k; measurement noise covariance matrix R k; in the presence of control actions - the matrix of their coefficients B k .

Filter operation illustration. Matrices are marked with squares. Ellipses mark matrices of multivariate normal distributions (including means and covariances). Vectors are left uncircled. In the simplest case, some matrices do not change in time (do not depend on the index k), but are still used by the filter in each cycle of operation.

The system/process model implies that the true state at the moment k obtained from the true state at the moment k−1 according to the equation:

,

• F k- process/system evolution matrix that affects the vector x k−1 (state vector at the moment k−1 );
• B k- control matrix, which is applied to the vector of control actions u k ;
• w k- normal random process with zero mathematical expectation and covariance matrix Q k, which describes the random nature of the system/process evolution:

In the moment k observation (measurement) z k true state vector x k, which are interconnected by the equation:

where H k- measurement matrix linking the true state vector and the vector of measurements made, v k- white Gaussian measurement noise with zero mean and covariance matrix R k :

Initial state and vectors of random processes on each cycle ( x 0 , w 1 , …, w k , v 1 , …, v k) are considered independent.

Many real dynamical systems cannot be accurately described by this model. In practice, the dynamics not taken into account in the model can seriously spoil the performance of the filter, especially when working with an unknown stochastic signal at the input. Moreover, dynamics not taken into account in the model can make the filter unstable. On the other hand, independent white noise as a signal will not cause the algorithm to diverge. The task of separating measurement noise from dynamics unaccounted for in the model is difficult; it is solved using the theory of robust control systems.

Kalman filter

The Kalman filter is a type of recursive filter. To calculate the estimate of the state of the system for the current cycle of work, it needs an estimate of the state (in the form of an estimate of the state of the system and an estimate of the error in determining this state) at the previous cycle of work and measurements at the current cycle. This property distinguishes it from packet filters, which require knowledge of the history of measurements and/or evaluations in the current cycle of operation. Further, by writing we mean the estimate of the true vector at the moment n taking into account measurements from the moment the work began and until the moment m inclusive.

The filter state is set by two variables:

Iterations of the Kalman filter are divided into two phases: extrapolation and correction. During extrapolation, the filter receives a preliminary estimate of the state of the system (in the Russian-language literature it is often denoted , where means "extrapolation", and k- the number of the cycle at which it was received) for the current step according to the final assessment of the state from the previous step (or a preliminary assessment for the next cycle according to the final assessment of the current step, depending on the interpretation). This preliminary estimate is also called the prior state estimate, since observations of the corresponding step are not used to obtain it. In the correction phase, the a priori extrapolation is supplemented with relevant current measurements to correct the estimate. The adjusted estimate is also called the posterior state estimate, or simply the state vector estimate. Usually these two phases alternate: extrapolation is performed based on the results of the correction until the next observation, and the correction is performed together with the observations available at the next step, etc. However, another development of events is possible, if for some reason the observation turned out to be inaccessible, then the correction stage may be skipped and extrapolated from the unadjusted estimate (a priori extrapolation). Similarly, if independent measurements are available only in certain cycles of work, corrections are still possible (usually using a different matrix of observations H k ).

extrapolation step

Correction stage

Deviation received per step k observations from the observation expected when extrapolating:
Covariance matrix for the deviation vector (error vector):
The Kalman-optimal gain matrix formed based on the covariance matrices of the available state vector extrapolation and the obtained measurements (via the deviation vector covariance matrix):
Correction of the previously obtained extrapolation of the state vector - obtaining an estimate of the state vector of the system:
Calculation of the covariance matrix for estimating the system state vector:

The expression for the covariance matrix for estimating the system state vector is valid only when using the reduced optimal vector of coefficients. In general, this expression has a more complex form.

Invariants

If the model is absolutely accurate and the initial conditions and are absolutely exactly specified, then the following values ​​are preserved after any number of iterations of the filter operation - they are invariants:

Mathematical expectations of estimates and extrapolations of the system state vector, error matrices are null vectors:

where is the mathematical expectation.

The calculated covariance matrices of extrapolations, estimates of the state of the system and the error vector coincide with the true covariance matrices:

An example of building a filter

Imagine a trolley standing on infinitely long rails in the absence of friction. Initially, it rests in position 0, but under the influence of random factors, random acceleration acts on it. We measure the position of the trolley every ∆ t seconds, but the measurements are inaccurate. We want to get estimates of the position of the cart and its speed. Let's apply the Kalman filter to this problem and determine all the necessary matrices.

In this problem, the matrices F , H , R and Q do not depend on time, we omit their indices. In addition, we do not control the trolley, so the control matrix B missing.

The coordinate and speed of the trolley is described by a vector in the linear state space

where is the speed (the first derivative of the coordinate with respect to time).

We will assume that between k−1 )th and k-th cycles the trolley moves with constant acceleration a k, distributed according to the normal law with zero mathematical expectation and standard deviation σ a. According to Newtonian mechanics, one can write

.

Covariance matrix of random influences

(σ a- scalar).

At each cycle of work, the position of the trolley is measured. Let us assume that the measurement error v k has a normal distribution with zero mean and standard deviation σz. Then

and the observational noise covariance matrix has the form

.

The initial position of the trolley is known exactly

, .

If the position and speed of the trolley are known only approximately, then the dispersion matrix can be initialized with a sufficiently large number L, so that the number exceeds the dispersion of measurements of the coordinate

, .

In this case, in the first cycles of operation, the filter will use the measurement results with more weight than the available a priori information.

Derivation of formulas

State vector estimation covariance matrix

By definition of the covariance matrix P k|k

we substitute the expression for estimating the state vector

and write the expression for the error vector

and measurement vector

take out the measurement error vector v k

since the measurement error vector v k not correlated with other arguments, we get the expression

in accordance with the properties of the covariance of vectors, this expression is transformed to the form

replacing the expression for the state vector extrapolation covariance matrix with P k|k−1 and determination of the covariance matrix of observational noise on R k, we get

The resulting expression is valid for an arbitrary matrix of coefficients, but if it is the matrix of coefficients that is Kalman optimal, then this expression for the covariance matrix can be simplified.

Optimal Gain Matrix

The Kalman filter minimizes the sum of squares of the expected state vector estimation errors.

State vector estimation error vector

The task is to minimize the sum of mathematical expectations of the squares of the components of a given vector

,

which is equivalent to minimizing the trace of the covariance matrix of the state vector estimate P k|k. Let us substitute the available expressions into the expression for the covariance matrix of the state vector estimation and complete it to the full square:

Note that the last term is the covariance matrix of some random variable, so its trace is non-negative. The minimum trace is reached when the last term is set to zero:

It is claimed that this matrix is ​​the desired one and, when used as a matrix of coefficients in the Kalman filter, minimizes the sum of the mean squares of state vector estimation errors.

Covariance matrix of the state vector estimation when using the optimal matrix of coefficients

Expression for the covariance matrix of the state vector estimation P k|k when using the optimal matrix of coefficients will take the form:

This formula is computationally simpler and therefore is almost always used in practice, but it is correct only when using the optimal matrix of coefficients. If, due to low computational accuracy, there is a problem with computational stability, or a non-optimal coefficient matrix is ​​specifically used, the general formula for the state vector estimation covariance matrix should be used.

Wiener filters are best suited for processing processes or segments of processes as a whole (block processing). Sequential processing requires a current estimate of the signal at each cycle, taking into account the information received at the filter input during the observation process.

With Wiener filtering, each new signal sample would require recalculation of all filter weights. Currently, adaptive filters are widely used, in which incoming new information is used to continuously correct the previously made signal estimate (target tracking in radar, automatic control systems in control, etc.). Of particular interest are adaptive filters of the recursive type, known as the Kalman filter.

These filters are widely used in control loops in automatic regulation and control systems. That is where they came from, as evidenced by such specific terminology used in describing their work as the state space.

One of the main tasks that need to be solved in the practice of neural computing is to obtain fast and reliable neural network learning algorithms. In this regard, it may be useful to use a learning algorithm of linear filters in the feedback loop. Since learning algorithms are iterative in nature, such a filter must be a sequential recursive estimator.

Parameter Estimation Problem

One of the problems of the theory of statistical solutions, which is of great practical importance, is the problem of estimating the state vectors and parameters of systems, which is formulated as follows. Suppose it is necessary to estimate the value of the vector parameter $X$, which is inaccessible to direct measurement. Instead, another parameter $Z$ is measured, depending on $X$. The task of estimation is to answer the question: what can be said about $X$ given $Z$. In the general case, the procedure for optimal estimation of the vector $X$ depends on the accepted quality criterion for the estimation.

For example, the Bayesian approach to the parameter estimation problem requires complete a priori information about the probabilistic properties of the estimated parameter, which is often impossible. In these cases, one resorts to the method of least squares (LSM), which requires much less a priori information.

Let us consider the application of least squares for the case when the observation vector $Z$ is connected with the parameter estimation vector $X$ by a linear model, and there is a noise $V$ in the observation that is not correlated with the estimated parameter:

$Z = HX + V$, (1)

where $H$ is the transformation matrix describing the relationship between the observed values ​​and the estimated parameters.

The estimate $X$ minimizing the squared error is written as follows:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Let the noise $V$ be uncorrelated, in which case the matrix $R_V$ is just the identity matrix, and the estimation equation becomes simpler:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

Recording in matrix form greatly saves paper, but may be unusual for someone. The following example, taken from Yu. M. Korshunov's monograph "Mathematical Foundations of Cybernetics", illustrates all this.
There is the following electrical circuit:

The observed values ​​in this case are the instrument readings $A_1 ​​= 1 A, A_2 = 2 A, V = 20 B$.

In addition, the resistance $R = 5$ Ohm is known. It is required to estimate in the best way, from the point of view of the minimum mean square error criterion, the values ​​of currents $I_1$ and $I_2$. The most important thing here is that there is some relationship between the observed values ​​(instrument readings) and the estimated parameters. And this information is brought in from outside.

In this case, these are Kirchhoff's laws, in the case of filtering (which will be discussed later) - an autoregressive time series model, which assumes that the current value depends on the previous ones.

So, knowledge of Kirchhoff's laws, which is in no way connected with the theory of statistical decisions, allows you to establish a connection between the observed values ​​and the estimated parameters (those who studied electrical engineering can check, the rest will have to take their word for it):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

This is in vector form:

$$\begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) \begin(vmatrix) I_1\ \ I_2 \end(vmatrix) + \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Or $Z = HX + V$, where

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Considering the noise values ​​as uncorrelated with each other, we find the estimate of I 1 and I 2 by the least squares method in accordance with formula 3:

$H^TH= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) = \ begin(vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 \\ 2\\ 4 \end(vmatrix) = \begin(vmatrix) 7\ \ 10 \end(vmatrix) ; X(vmatrix)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1)(6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

So $I_1 = 5/6 = 0.833 A$; $I_2 = 9/6 = 1.5 A$.

Filtering task

In contrast to the problem of estimating parameters that have fixed values, in the filtration problem it is required to evaluate processes, that is, to find current estimates of a time-varying signal distorted by noise and, therefore, inaccessible to direct measurement. In the general case, the type of filtering algorithms depends on the statistical properties of the signal and noise.

We will assume that the useful signal is a slowly varying function of time, and the noise is uncorrelated noise. We will use the least squares method, again due to the lack of a priori information about the probabilistic characteristics of the signal and noise.

First, we obtain an estimate of the current value of $x_n$ using the last $k$ values ​​of the time series $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1))$. The observation model is the same as in the parameter estimation problem:

It is clear that $Z$ is a column vector consisting of the observed values ​​of the time series $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1))$, $V $ – noise column vector $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi_(n-(k-1))$, distorting the true signal. And what do the symbols $H$ and $X$ mean? What kind of column vector $X$, for example, can we talk about if all that is needed is to give an estimate of the current value of the time series? And what is meant by the transformation matrix $H$ is not at all clear.

All these questions can be answered only if the concept of a signal generation model is introduced into consideration. That is, some model of the original signal is needed. This is understandable, in the absence of a priori information about the probabilistic characteristics of the signal and noise, it remains only to make assumptions. You can call it fortune-telling on the coffee grounds, but experts prefer a different terminology. In their hair dryer, this is called a parametric model.

In this case, the parameters of this particular model are evaluated. When choosing an appropriate signal generation model, remember that any analytical function can be expanded in a Taylor series. The striking property of the Taylor series is that the form of a function at any finite distance $t$ from some point $x=a$ is uniquely determined by the behavior of the function in an infinitely small neighborhood of the point $x=a$ (we are talking about its first and higher order derivatives ).

Thus, the existence of Taylor series means that the analytic function has an internal structure with a very strong connection. If, for example, we restrict ourselves to three members of the Taylor series, then the signal generation model will look like this:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatrix) $$

That is, formula 4, with a given order of the polynomial (in the example it is equal to 2), establishes a connection between the $n$-th value of the signal in the time sequence and $(n-i)$-th. Thus, the estimated state vector in this case includes, in addition to the estimated value itself, the first and second derivatives of the signal.

In automatic control theory, such a filter would be called a second-order astatic filter. The transformation matrix $H$ for this case (the estimate is based on the current and $k-1$ previous samples) looks like this:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \ end(vmatrix)$$

All these numbers are obtained from the Taylor series, assuming that the time interval between adjacent observed values ​​is constant and equal to 1.

Thus, the filtering problem, under our assumptions, has been reduced to the problem of estimating parameters; in this case, the parameters of the signal generation model adopted by us are estimated. And the evaluation of the values ​​of the state vector $X$ is carried out according to the same formula 3:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

In fact, we have implemented a parametric estimation process based on an autoregressive model of the signal generation process.

Formula 3 is easily implemented in software, for this you need to fill in the matrix $H$ and the vector column of observations $Z$. Such filters are called finite memory filters, since they use the last $k$ observations to get the current estimate $X_(not)$. At each new observation step, a new set of observations is added to the current set of observations and the old is discarded. This evaluation process is called sliding window.

Growing Memory Filters

Filters with finite memory have the main disadvantage that after each new observation, it is necessary to re-compute a complete recalculation of all data stored in memory. In addition, the calculation of estimates can be started only after the results of the first $k$ observations have been accumulated. That is, these filters have a long duration of the transient process.

To deal with this shortcoming, it is necessary to move from a filter with permanent memory to a filter with growing memory. In such a filter, the number of observed values ​​to be evaluated must match the number n of the current observation. This makes it possible to obtain estimates starting from the number of observations equal to the number of components of the estimated vector $X$. And this is determined by the order of the adopted model, that is, how many terms from the Taylor series are used in the model.

At the same time, as n increases, the smoothing properties of the filter improve, that is, the accuracy of the estimates increases. However, the direct implementation of this approach is associated with an increase in computational costs. Therefore, growing memory filters are implemented as recurrent.

The point is that by time n we already have the estimate $X_((n-1)ots)$, which contains information about all previous observations $z_n, z_(n-1), z_(n-2) \dots z_(n-(k-1))$. The estimate $X_(not)$ is obtained by the next observation $z_n$ using the information stored in the estimate $X_((n-1))(\mbox (ot))$. This procedure is called recurrent filtering and consists of the following:

• according to the estimate $X_((n-1))(\mbox (ots))$, the estimate $X_n$ is predicted by formula 4 for $i = 1$: $X_(\mbox (noca priori)) = F_1X_((n-1 )ots)$. This is an a priori estimate;
• according to the results of the current observation $z_n$, this a priori estimate is turned into a true one, that is, a posteriori;
• this procedure is repeated at each step, starting from $r+1$, where $r$ is the filter order.

The final recursive filtering formula looks like this:

$X_((n-1)ots) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

where for our second order filter:

The growing memory filter, which works according to formula 6, is a special case of the filtering algorithm known as the Kalman filter.

In the practical implementation of this formula, it must be remembered that the a priori estimate included in it is determined by formula 4, and the value $h_0 X_(\mbox (nocapriori))$ is the first component of the vector $X_(\mbox (nocapriori))$.

The growing memory filter has one important feature. Looking at Formula 6, the final score is the sum of the predicted score vector and the correction term. This correction is large for small $n$ and decreases as $n$ increases, tending to zero as $n \rightarrow \infty$. That is, as n grows, the smoothing properties of the filter grow and the model embedded in it begins to dominate. But the real signal can correspond to the model only in some areas, so the accuracy of the forecast deteriorates.

To combat this, starting from some $n$, a ban is imposed on further reduction of the correction term. This is equivalent to changing the filter band, that is, for small n, the filter is more broadband (less inertial), for large n, it becomes more inertial.

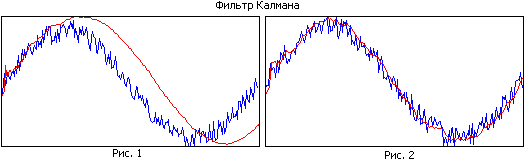
Compare Figure 1 and Figure 2. In the first figure, the filter has a large memory, while it smoothes well, but due to the narrow band, the estimated trajectory lags behind the real one. In the second figure, the filter memory is smaller, it smooths worse, but it tracks the real trajectory better.

Literature

1. Yu.M.Korshunov "Mathematical Foundations of Cybernetics"
2. A.V.Balakrishnan "Kalman filtration theory"
3. V.N. Fomin "Recurrent estimation and adaptive filtering"
4. C.F.N. Cowen, P.M. Grant "Adaptive filters"

In the process of automation of technological processes for the control of mechanisms and units, one has to deal with measurements of various physical quantities. This can be pressure and flow of a liquid or gas, rotational speed, temperature, and much more. Measurement of physical quantities is carried out using analog sensors. An analog signal is a data signal in which each of the representing parameters is described by a function of time and a continuous set of possible values. It follows from the continuity of the value space that any interference introduced into the signal is indistinguishable from the useful signal. Therefore, the analog input of the control device will receive an incorrect value of the required physical quantity. Therefore, it is necessary to filter the signal coming from the sensor.

One of the effective filtering algorithms is the Kalman filter. The Kalman filter is a recursive filter that estimates the state vector of a dynamical system using a series of incomplete and noisy measurements. The Kalman filter uses a dynamic model of the system (for example, the physical law of motion), control actions and a set of successive measurements to form an optimal state estimate. The algorithm consists of two iterative phases: prediction and correction. At the first stage, the prediction of the state at the next point in time is calculated (taking into account the inaccuracy of their measurement). In the second, new information from the sensor corrects the predicted value (also taking into account the inaccuracy and noise of this information).

During the prediction phase:

1. System State Prediction:

where is the prediction of the state of the system at the current time; – matrix of transition between states (dynamic model of the system); – prediction of the state of the system at the previous moment of time; – matrix of control action application; is the control action at the previous moment of time.

1. Covariance error prediction:

where is the error prediction; – error at the previous moment of time; is the process noise covariance.

During the adjustment phase:

1. Kalman Gain Calculation:

where is the Kalman gain; – matrix of measurements, displaying the ratio of measurements and states; is the measurement noise covariance.

where is the measurement at the current time.

1. Covariance error update:

where is the identity matrix.

If the state of the system is described by a single variable, then = 1, and the matrices degenerate into ordinary equations.

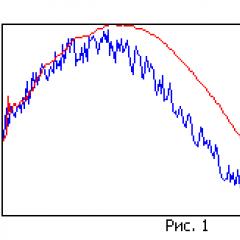
To clearly demonstrate the effectiveness of the Kalman filter, an experiment was conducted with the AVR PIC KY-037 volume sensor, which is connected to the Arduino Uno microcontroller. Figure 1 shows a graph of sensor readings without applying a filter (line 1). Chaotic fluctuations in the value at the output of the sensor indicate the presence of noise.

Figure 1. Graph of sensor readings without applying a filter

To apply the filter, it is necessary to determine the values ​​of the variables , and , which determine the dynamics of the system and measurements. We accept and equal to 1, and equal to 0, since there are no control actions in the system. To determine the smoothing properties of the filter, it is necessary to calculate the value of the variable and select the value of the parameter.

We will calculate the variable in Microsoft Excel 2010. To do this, it is necessary to calculate the standard deviation for a sample of sensor readings. = 0.62. is selected depending on the required level of filtration, we accept = 0.001. In Figure 2, the second line is a graph of the sensor readings using a filter.

Figure 2. Graph of sensor readings using the Kalman filter

From the graph, we can conclude that the filter coped with the task of filtering noise, since in the steady state, fluctuations in the sensor readings that have passed the filtering are insignificant.

However, the Kalman filter has a significant drawback. If the sensor's measured value can change rapidly, the filtered sensor reading will not change as quickly as the measured value. Figure 3 shows the response of the Kalman filter to a jump in the measured value.

Figure 3. Response of the Kalman filter to a jump in the measured value

The response of the filter to the jump in the measured value turned out to be insignificant. If the measured value changes significantly and then does not return to the previous value, then the filtered sensor readings will correspond to the real value of the measured value only after a significant period of time, which is unacceptable for automatic control systems that require high speed.

From the experiment, we can conclude that the Kalman filter should be used to filter sensor readings in low-speed systems.

Bibliography:

1. GOST 17657-79. Data transfer. Terms and Definitions. - Moscow: Publishing House of Standards, 2005. - 2 p.
2. Kalman filter // Wikipedia. . Date of update: 04/26/2017. URL: http://ru.wikipedia.org/?oldid=85061599 (date of access: 05/21/2017).

This filter is used in various fields - from radio engineering to economics. Here we will discuss the main idea, meaning, essence of this filter. It will be presented in the simplest possible language.
Let's suppose that we have a need to measure some quantities of some object. In radio engineering, most often they deal with measuring voltages at the output of a certain device (sensor, antenna, etc.). In the example with an electrocardiograph (see), we are dealing with measurements of biopotentials on the human body. In economics, for example, the measured value can be exchange rates. Every day the exchange rate is different, i.е. every day "his measurements" give us a different value. And to generalize, we can say that most of human activity (if not all) comes down to constant measurements-comparisons of certain quantities (see the book).
So let's say we measure something all the time. Let's also assume that our measurements always come with some error - this is understandable, because there are no ideal measuring instruments, and everyone gives a result with an error. In the simplest case, this can be reduced to the following expression: z=x+y, where x is the true value that we want to measure and would measure if we had an ideal measuring device, y is the measurement error introduced by the measuring device, and z is the value we measured. So the task of the Kalman filter is to still guess (determine) from the z we measured, what was the true value of x when we got our z (in which the true value and the measurement error "sit"). It is necessary to filter (screen out) the true value of x from z - remove the distorting noise y from z. That is, having only the amount on hand, we need to guess which terms gave this amount.
In the light of the above, we now formulate everything as follows. Let there be only two random numbers. We are given only their sum and we are required to determine from this sum what the terms are. For example, we were given the number 12 and they say: 12 is the sum of the numbers x and y, the question is what x and y are equal to. To answer this question, we make the equation: x+y=12. We got one equation with two unknowns, therefore, strictly speaking, it is not possible to find two numbers that gave this sum. But we can still say something about these numbers. We can say that it was either the numbers 1 and 11, or 2 and 10, or 3 and 9, or 4 and 8, etc., it is also either 13 and -1, or 14 and -2, or 15 and -3 etc. That is, by the sum (in our example 12) we can determine the set of possible options that give exactly 12 in total. One of these options is the pair we are looking for, which actually gave 12 right now. It is also worth noting that all variants of pairs of numbers giving in the sum 12 form a straight line shown in Fig. 1, which is given by the equation x+y=12 (y=-x+12).

Fig.1

Thus, the pair we are looking for lies somewhere on this straight line. I repeat, it is impossible to choose from all these options the pair that actually existed - which gave the number 12, without having any additional clues. However, in the situation for which the Kalman filter was invented, there are such hints. There is something known in advance about random numbers. In particular, the so-called distribution histogram for each pair of numbers is known there. It is usually obtained after sufficiently long observations of the fallout of these very random numbers. That is, for example, it is known from experience that in 5% of cases the pair x=1, y=8 usually falls out (we denote this pair as follows: (1,8)), in 2% of cases the pair x=2, y=3 ( 2.3), in 1% of cases a couple (3.1), in 0.024% of cases a couple (11.1), etc. Again, this histogram is set for all couples numbers, including those that add up to 12. Thus, for each pair that adds up to 12, we can say that, for example, the pair (1, 11) falls out in 0.8% of the cases, the pair ( 2, 10) - in 1% of cases, pair (3, 9) - in 1.5% of cases, etc. Thus, we can determine from the histogram in what percentage of cases the sum of the terms of the pair is 12. Let, for example, in 30% of cases the sum gives 12. And in the remaining 70%, the remaining pairs fall out - these are (1.8), (2, 3), (3,1), etc. - those that add up to numbers other than 12. Moreover, let, for example, a pair (7.5) fall out in 27% of cases, while all other pairs that give a total of 12 fall out in 0.024% + 0.8% +1%+1.5%+…=3% of cases. So, according to the histogram, we found out that numbers giving a total of 12 fall out in 30% of cases. At the same time, we know that if 12 fell out, then most often (27% of 30%) the reason for this is a pair (7.5). That is, if already 12 rolled, we can say that in 90% (27% of 30% - or, what is the same, 27 times out of every 30) the reason for the roll of 12 is a pair (7.5). Knowing that the pair (7.5) is most often the reason for getting the sum equal to 12, it is logical to assume that, most likely, it fell out now. Of course, it’s still not a fact that the number 12 is actually formed by this particular pair, however, next time, if we come across 12, and we again assume a pair (7.5), then somewhere in 90% of cases We are 100% right. But if we assume a pair (2, 10), we will be right only 1% of 30% of the time, which is equal to 3.33% of correct guesses compared to 90% when guessing a pair (7,5). That's all - this is the point of the Kalman filter algorithm. That is, the Kalman filter does not guarantee that it will not make a mistake in determining the summand, but it guarantees that it will make a mistake the minimum number of times (the probability of an error will be minimal), since it uses statistics - a histogram of falling out of pairs of numbers. It should also be emphasized that the so-called probability distribution density (PDD) is often used in the Kalman filtering algorithm. However, it must be understood that the meaning there is the same as that of the histogram. Moreover, a histogram is a function built on the basis of PDF and being its approximation (see, for example, ).
In principle, we can depict this histogram as a function of two variables - that is, as a kind of surface above the xy plane. Where the surface is higher, the probability of the corresponding pair falling out is also higher. Figure 2 shows such a surface.

fig.2

As you can see, above the line x + y = 12 (which are variants of pairs giving a total of 12), there are surface points at different heights and the highest height is in the variant with coordinates (7,5). And when we come across a sum equal to 12, in 90% of cases the pair (7,5) is the reason for the appearance of this sum. Those. it is this pair, which adds up to 12, that has the highest probability of occurring, provided that the sum is 12.
Thus, the idea behind the Kalman filter is described here. It is on it that all sorts of its modifications are built - single-step, multi-step recurrent, etc. For a deeper study of the Kalman filter, I recommend the book: Van Tries G. Theory of detection, estimation and modulation.

p.s. For those who are interested in explaining the concepts of mathematics, what is called "on the fingers", we can recommend this book and, in particular, the chapters from its "Mathematics" section (you can purchase the book itself or individual chapters from it).