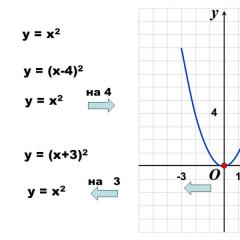
How to construct the function ax2 bx c. Determining the values ​​of the coefficients of a quadratic function from a graph. something is to discover for yourself

As practice shows, tasks on the properties and graphs of a quadratic function cause serious difficulties. This is quite strange, because they study the quadratic function in the 8th grade, and then throughout the first quarter of the 9th grade they “torment” the properties of the parabola and build its graphs for various parameters.

This is due to the fact that when forcing students to construct parabolas, they practically do not devote time to “reading” the graphs, that is, they do not practice comprehending the information received from the picture. Apparently, it is assumed that, after constructing a dozen or two graphs, a smart student himself will discover and formulate the relationship between the coefficients in the formula and the appearance of the graph. In practice this does not work. For such a generalization, serious experience in mathematical mini-research is required, which most ninth-graders, of course, do not possess. Meanwhile, the State Inspectorate proposes to determine the signs of the coefficients using the schedule.

We will not demand the impossible from schoolchildren and will simply offer one of the algorithms for solving such problems.

So, a function of the form y = ax 2 + bx + c called quadratic, its graph is a parabola. As the name suggests, the main term is ax 2. That is A should not be equal to zero, the remaining coefficients ( b And With) can equal zero.

Let's see how the signs of its coefficients affect the appearance of a parabola.

The simplest dependence for the coefficient A. Most schoolchildren confidently answer: “if A> 0, then the branches of the parabola are directed upward, and if A < 0, - то вниз". Совершенно верно. Ниже приведен график квадратичной функции, у которой A > 0.

y = 0.5x 2 - 3x + 1

In this case A = 0,5

And now for A < 0:

y = - 0.5x2 - 3x + 1

In this case A = - 0,5

Impact of the coefficient With It's also pretty easy to follow. Let's imagine that we want to find the value of a function at a point X= 0. Substitute zero into the formula:

y = a 0 2 + b 0 + c = c. It turns out that y = c. That is With is the ordinate of the point of intersection of the parabola with the y-axis. Typically, this point is easy to find on the graph. And determine whether it lies above zero or below. That is With> 0 or With < 0.

With > 0:

y = x 2 + 4x + 3

With < 0

y = x 2 + 4x - 3

Accordingly, if With= 0, then the parabola will necessarily pass through the origin:

y = x 2 + 4x

More difficult with the parameter b. The point at which we will find it depends not only on b but also from A. This is the top of the parabola. Its abscissa (axis coordinate X) is found by the formula x in = - b/(2a). Thus, b = - 2ax in. That is, we proceed as follows: we find the vertex of the parabola on the graph, determine the sign of its abscissa, that is, we look to the right of zero ( x in> 0) or to the left ( x in < 0) она лежит.

However, that's not all. We also need to pay attention to the sign of the coefficient A. That is, look at where the branches of the parabola are directed. And only after that, according to the formula b = - 2ax in determine the sign b.

Let's look at an example:

The branches are directed upwards, which means A> 0, the parabola intersects the axis at below zero, that is With < 0, вершина параболы лежит правее нуля. Следовательно, x in> 0. So b = - 2ax in = -++ = -. b < 0. Окончательно имеем: A > 0, b < 0, With < 0.

Algebra lesson notes for 8th grade secondary school

Lesson topic: Function

The purpose of the lesson:

· Educational: define the concept of a quadratic function of the form (compare graphs of functions and ), show the formula for finding the coordinates of the vertex of a parabola (teach how to apply this formula in practice); to develop the ability to determine the properties of a quadratic function from a graph (finding the axis of symmetry, the coordinates of the vertex of a parabola, the coordinates of the points of intersection of the graph with the coordinate axes).

· Developmental: development of mathematical speech, the ability to correctly, consistently and rationally express one’s thoughts; developing the skill of correctly writing mathematical text using symbols and notations; development of analytical thinking; development of students’ cognitive activity through the ability to analyze, systematize and generalize material.

· Educational: fostering independence, the ability to listen to others, developing accuracy and attention in written mathematical speech.

Lesson type: learning new material.

Teaching methods:

generalized reproductive, inductive heuristic.

Requirements for students' knowledge and skills

know what a quadratic function of the form is, the formula for finding the coordinates of the vertex of a parabola; be able to find the coordinates of the vertex of a parabola, the coordinates of the points of intersection of the graph of a function with the coordinate axes, and use the graph of a function to determine the properties of a quadratic function.

Equipment:

Lesson Plan

I. Organizational moment (1-2 min)

II. Updating knowledge (10 min)

III. Presentation of new material (15 min)

IV. Consolidating new material (12 min)

V. Summing up (3 min)

VI. Homework assignment (2 min)

During the classes

I. Organizational moment

Greeting, checking absentees, collecting notebooks.

II. Updating knowledge

Teacher: In today's lesson we will study a new topic: "Function". But first, let's repeat the previously studied material.

Frontal survey:

1) What is called a quadratic function? (A function where given real numbers, , is a real variable, is called a quadratic function.)

2) What is the graph of a quadratic function? (The graph of a quadratic function is a parabola.)

3) What are the zeros of a quadratic function? (The zeros of a quadratic function are the values ​​at which it becomes zero.)

4) List the properties of the function. (The values ​​of the function are positive at and equal to zero at; the graph of the function is symmetrical with respect to the ordinate axes; at - the function increases, at - decreases.)

5) List the properties of the function. (If , then the function takes positive values ​​at , if , then the function takes negative values ​​at , the value of the function is only 0; the parabola is symmetrical about the ordinate axis; if , then the function increases at and decreases at , if , then the function increases at , decreases – at .)

III. Presentation of new material

Teacher: Let's start learning new material. Open your notebooks, write down the date and topic of the lesson. Pay attention to the board.

Writing on the board: Number.

Function.

Teacher: On the board you see two graphs of functions. The first graph, and the second. Let's try to compare them.

You know the properties of the function. Based on them, and comparing our graphs, we can highlight the properties of the function.

So, what do you think will determine the direction of the branches of the parabola?

Students: The direction of the branches of both parabolas will depend on the coefficient.

Teacher: Absolutely right. You can also notice that both parabolas have an axis of symmetry. In the first graph of the function, what is the axis of symmetry?

Students: For a parabola, the axis of symmetry is the ordinate axis.

Teacher: Right. What is the axis of symmetry of a parabola?

Students: The axis of symmetry of a parabola is the line that passes through the vertex of the parabola, parallel to the ordinate axis.

Teacher: Right. So, the axis of symmetry of the graph of a function will be called a straight line passing through the vertex of the parabola, parallel to the ordinate axis.

And the vertex of a parabola is a point with coordinates . They are determined by the formula:

Write the formula in your notebook and circle it in a frame.

Writing on the board and in notebooks

Coordinates of the vertex of the parabola.

Teacher: Now, to make it more clear, let's look at an example.

Example 1: Find the coordinates of the vertex of the parabola .

Solution: According to the formula

Teacher: As we have already noted, the axis of symmetry passes through the vertex of the parabola. Look at the blackboard. Draw this picture in your notebook.

Write on the board and in notebooks:

Teacher: In the drawing: - equation of the axis of symmetry of a parabola with the vertex at the point where the abscissa is the vertex of the parabola.

Let's look at an example.

Example 2: Using the graph of the function, determine the equation for the axis of symmetry of the parabola.

The equation for the axis of symmetry has the form: , which means the equation for the axis of symmetry of this parabola is .

Answer: - equation of the axis of symmetry.

IV. Consolidation of new material

Teacher: The tasks that need to be solved in class are written on the board.

Writing on the board: № 609(3), 612(1), 613(3)

Teacher: But first, let's solve an example not from the textbook. We will decide at the board.

Example 1: Find the coordinates of the vertex of a parabola

Solution: According to the formula

Answer: coordinates of the vertex of the parabola.

Example 2: Find the coordinates of the intersection points of the parabola with coordinate axes.

Solution: 1) With axis:

Those.

According to Vieta's theorem:

The points of intersection with the x-axis are (1;0) and (2;0).

2) With axle:

The point of intersection with the ordinate axis (0;2).

Answer: (1;0), (2;0), (0;2) – coordinates of the points of intersection with the coordinate axes.